深度学习笔记

[TOC]

神经网络和深度学习(Neural Networks and Deep Learning)

神经网络

SNN

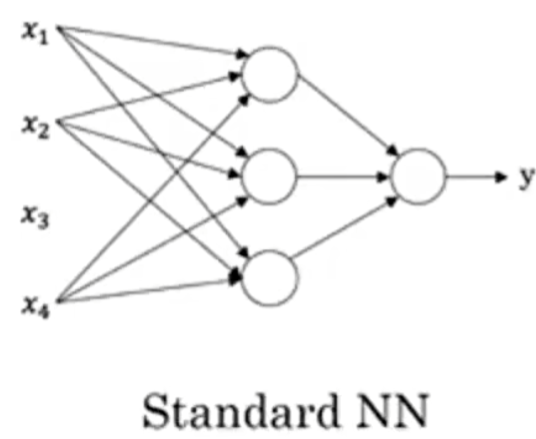
这就是一个简单的神经网络，其中的每一个箭头就代表一个ReLU函数

监督学习

数据

结构化数据：表格

非结构化数据：文本、图像、音频

深度学习兴起

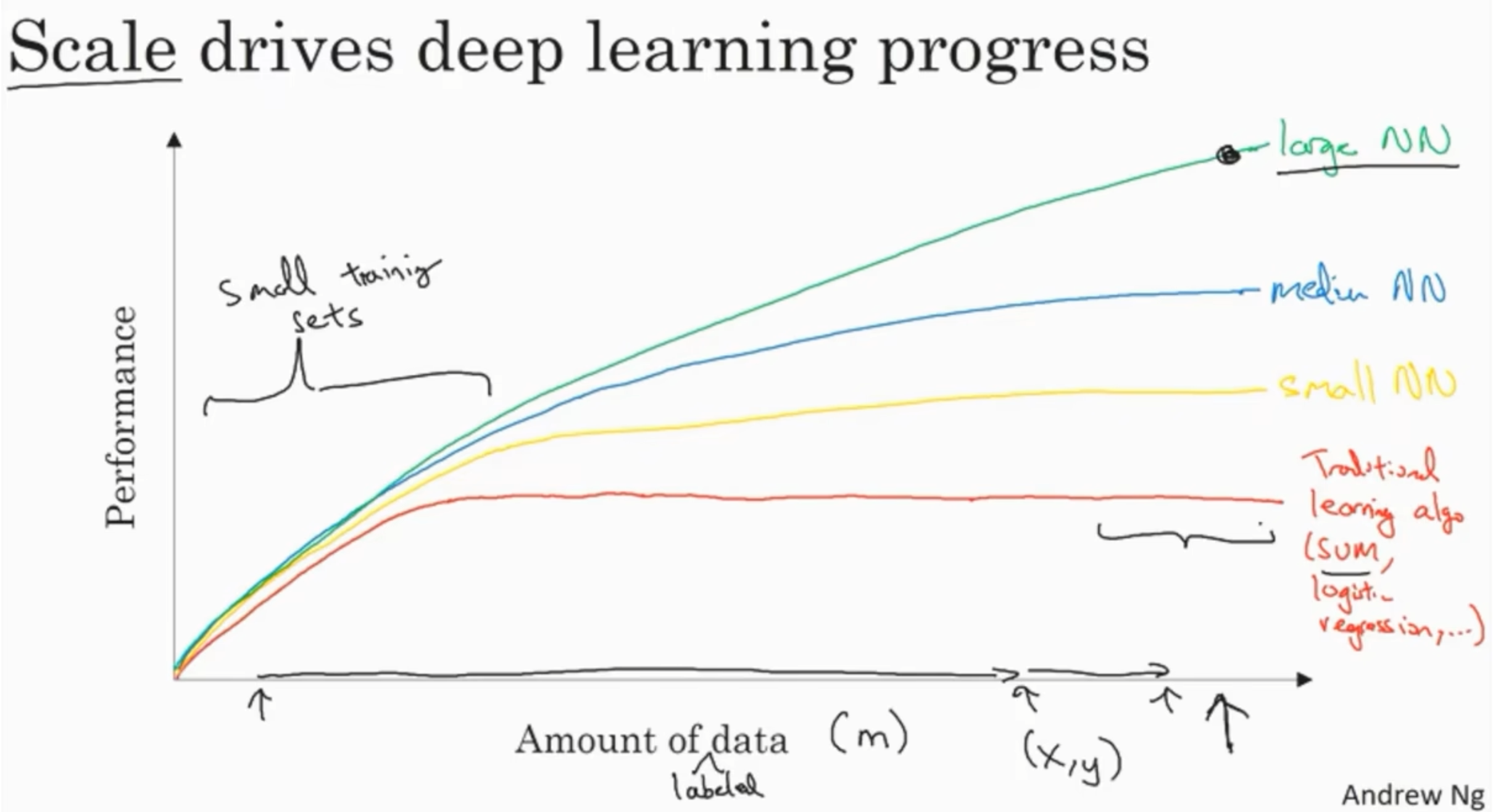
神经网络越大、数据集越大，神经网络性能越好。

数据集不够大的时候，自己提取出来的特征和算法实现细节决定了算法的性能和表现。

神经网络的编程基础(Basics of Neural Network programming)

二分分类

一些符号

：表示一个维数据，为输入数据，维度为；

：表示输出结果，取值为；

：表示第组数据，可能是训练数据，也可能是测试数据，此处默认为训练数据；

一个单独的样本：，是维矩阵的特征向量，

训练集将由个训练样本组成，其中表示第一个样本的输入和输出，表示第二个样本的输入和输出，直到最后一个样本，然后所有的这些一起表示整个训练集。

有时候为了强调这是训练样本的个数，会写作，当涉及到测试集的时候，我们会使用来表示测试集的样本数

表示一个训练集，表示一个测试集的样本数

，是一个的矩阵，表示一个训练集。在Python中：X.shape 用于输出矩阵的维度，X.shape =

，表示输出，Y.shape = (1,m)

Logistic回归

给定信息

给定: ，我们希望

参数

，拦截器，把b和w视为独立的参数会更好

输出

Sigmoid函数

Sigmoid函数定义为：
当很大时，
当为大负数时，

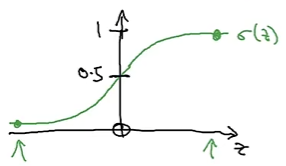
Sigmoid函数的图像

Sigmoid函数具有S形曲线，将任何输入映射到0和1之间的值。
- 当很大时，
- 当为大负数时，

重要说明

对于大的，
对于大的负数， $大数字$

逻辑回归的代价函数（Logistic Regression Cost Function）

需要一个代价函数，通过训练代价函数来得到参数和参数。

逻辑回归成本函数

预测值：
$其中$
给定数据集，我们希望：

损失（误差）函数（单个样本）

Logistic回归的损失函数：
称为损失函数，来衡量预测输出值和实际值有多接近。一般我们用预测值和实际值的平方差或者它们平方差的一半,但是通常在逻辑回归中我们不这么做，因为当我们在学习逻辑回归参数的时候，会发现我们的优化目标不是凸优化，只能找到多个局部最优值，梯度下降法很可能找不到全局最优值.
- 在逻辑回归中用到的损失函数是对数损失（交叉熵）：
当时：
$（我们希望较大）$
当时：
$（我们希望较小）$
在这门课中有很多的函数效果和现在这个类似，就是如果等于1，我们就尽可能让变大，如果等于0，我们就尽可能让变小。

成本函数（所有样本）

成本函数是所有样本的损失平均值：

Logistic回归可以被看做是一个非常小的神经网络

梯度下降法

假设函数为：

成本函数为：

其中，逻辑损失函数定义为：

目标：

我们希望找到能够最小化成本函数的和。

图示：

优化目标是最小化在三维空间中的值，如下图所示：

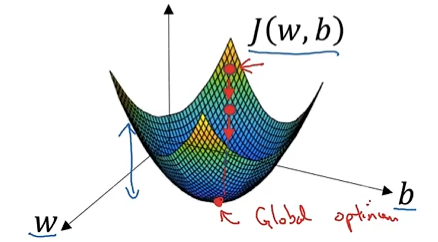
轴
轴
轴，红点为全局最小值。

因为函数是凸函数，无论在哪里初始化，应该达到同一点或大致相同的点。如果每次都选定从0开始不断下降直至找到全局最优解，则就叫梯度下降

梯度下降过程

在梯度下降过程中，随着每一步的更新，权重沿着负梯度方向更新，直到达到最小值。更新公式如下：

其中是学习率，决定了每次更新的步长。损失函数关于的梯度用于计算更新量。

同样，对于偏置，更新公式为：

图示：

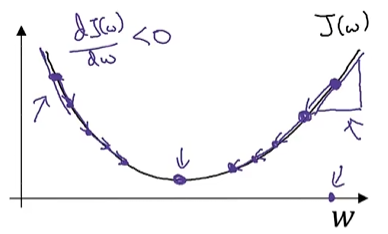
在图示中，展示了梯度下降的路径，沿着曲线的方向进行更新，每次迭代向着函数值更小的方向移动，直到达到最小值。

箭头指向梯度下降的方向。
目标是通过不断更新和，使得损失函数最小化。

在程序中dvar变量表示对最终值的导数

Logistic Regression 中的梯度下降（Logistic Regression Gradient Descent）

前向传播

输入特征的线性组合：

Sigmoid激活函数：
，其中

损失函数（二元交叉熵，单个样本）：
，其中是逻辑回归的输出，是样本的标签值。

代价函数：

计算图表示

x₁ x₂
| |
w₁ w₂
\ /
[z = w₁x₁ + w₂x₂ + b]
|
a = σ(z)
|
L(a,y)

反向传播导数

关键梯度计算

损失对输出的导数：
Sigmoid函数的导数：
链式法则求：

参数梯度

计算和变化对代价函数的影响

权重梯度：
偏置梯度：

关于单个样本的梯度下降算法，所需要做的就是如下的事情：

使用公式计算，
使用计算，计算，
来计算，
然后:
更新，
更新，
更新。

这就是关于单个样本实例的梯度下降算法中参数更新一次的步骤。

参数更新规则

梯度下降更新（学习率）：

实例演示

示例数据

假设输入样本和参数：

逐步计算

前向传播：
损失计算：
反向传播：
参数更新（学习率）：

关键理解

导数简化：最终梯度形式是Logistic回归的优美性质

向量化实现：实际代码中应使用：

1 2	dw = np.dot(X, (A-Y).T)/m db = np.sum(A-Y)/m

Logistic Regression on Examples

1. 成本函数（Cost Function）

逻辑回归的目标是最小化所有训练样本上的损失函数平均值，其成本函数定义为：

其中：

是 sigmoid 激活函数
是逻辑回归的交叉熵损失：

2. 目标函数的梯度计算

为了使用梯度下降法更新参数和，我们需要计算成本函数对每个参数的偏导数。

2.1 对的偏导

将损失函数代入并链式求导，得到：

因此：

2.2 对的偏导

3. 梯度下降算法实现（带循环）

初始化参数：

J = 0
dw1 = 0
dw2 = 0
db = 0

对于每个样本：

3.1 前向传播

3.2 损失和梯度计算

误差项：

累加梯度：

3.3 最终平均值

4. 参数更新（梯度下降）

给定学习率，使用以下规则更新参数：

代码流程

J=0;dw1=0;dw2=0;db=0;
for i = 1 to m
    z(i) = wx(i)+b;
    a(i) = sigmoid(z(i));
    J += -[y(i)log(a(i))+(1-y(i)）log(1-a(i));
    dz(i) = a(i)-y(i);
    dw1 += x1(i)dz(i);
    dw2 += x2(i)dz(i);
    db += dz(i);
J/= m;
dw1/= m;
dw2/= m;
db/= m;
w=w-alpha*dw
b=b-alpha*db

应用此方法在逻辑回归上你需要编写两个for循环。第一个for循环是一个小循环遍历个训练样本，第二个for循环是一个遍历所有特征的for循环。这是很低效的。

向量化（Vectorization）

基本概念

向量化是指将显式循环操作转换为矩阵/向量运算的过程，利用线性代数库（如NumPy）或硬件加速（如GPU）来提升计算效率。核心思想是用单条指令处理多条数据（SIMD）。

数学表达

非向量化实现
给定参数和输入，偏置，标量输出的计算为：

若和为二维向量：

循环示例
以下伪代码展示了非向量化的逐元素计算（效率低）：

z = 0
for i in range(log2(n - x)):
    z += ω[i] * x[i]  # 逐元素相乘累加
z += b

向量化实现

直接矩阵运算
使用库函数（如NumPy）将上述操作简化为：

其中等价于。
硬件加速
向量化计算可映射到GPU的SIMD（单指令多数据）架构：
$并行指令，高效处理批量数据$

实例说明

场景：计算批量数据的线性变换。

非向量化：需遍历每个样本和特征。
向量化：将数据堆叠为矩阵（为样本数），一次性计算：

其中为所有样本的输出向量。

优势总结

性能提升：减少显式循环，利用优化库和硬件并行能力。
代码简洁：数学表达式更贴近理论推导（如）。
扩展性：易于扩展到批量数据处理（如深度学习中的全连接层）。

向量与矩阵值函数的逐元素运算

基本概念

当需要对矩阵或向量的每个元素应用指数函数等逐元素运算时，数学表示为：
给定向量，其逐元素指数运算结果为。

Python实现示例

手动循环实现

import numpy as np

n = len(v)
u = np.zeros((n, 1))
for i in range(n):
    u[i] = math.exp(v[i])

使用NumPy内置函数

NumPy提供了高效的逐元素运算函数：

u = np.exp(v)       # 指数运算
u = np.log(v)       # 自然对数
u = np.abs(v)       # 绝对值（注：原图疑似误写为dx）
u = np.maximum(v, 0) # ReLU函数（逐元素取最大值）

逐元素运算的数学性质

线性与非线性的区别：
例如，是线性运算，而是非线性运算。
广播机制：
类似的运算会触发NumPy的广播规则，要求维度匹配或可广播。

应用场景

激活函数：如ReLU () 和Sigmoid（可通过指数实现）。
梯度计算：在反向传播中需处理逐元素导数的链式法则

在能够使用Numpy内置函数的时候尽量使用内置函数

向量化的示例应用

广播机制（Broadcasting）

原理
当操作不同维度的数组时，NumPy会自动扩展较小数组的维度以匹配大数组（无需显式复制数据）。例如：
$若则自动将扩展为$

实例
计算批量数据时，偏置会自动广播到每个样本：

import numpy as np
W = np.array([1, 2])    # shape (2,)
X = np.array([[1, 2], [3, 4]])  # shape (2,2)
b = 10
Z = np.dot(X, W) + b    # b被广播为 [10, 10]

向量化的梯度计算

理论推导
对于损失函数，其梯度计算也可向量化。设样本矩阵，标签：

代码实现

1 2	dW = np.dot(X.T, (Z - y)) / m # 向量化梯度 db = np.sum(Z - y) / m # 标量广播

避免常见错误

维度匹配
需确保矩阵乘法维度对齐。例如：
- 要求和同维度。
- 要求的列数等于的行数。
显式reshape
当输入维度不明确时，需手动调整：
1
x = x.reshape(-1, 1) # 确保列向量

实际案例：逻辑回归

假设函数
向量化实现Sigmoid激活：
损失函数

完整代码片段

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

Z = np.dot(W.T, X) + b
A = sigmoid(Z)
cost = -np.mean(Y * np.log(A) + (1 - Y) * np.log(1 - A))

性能对比

方法	时间（m=10,000）	代码复杂度
非向量化循环	2.3s	高
向量化	0.002s	低

注：向量化在数据量大时优势更显著，加速可达1000倍以上。

向量化逻辑回归的实现

Vectorizing Logistic Regression

单样本计算基础

对于单个样本，逻辑回归的前向传播步骤如下：

线性变换：
激活函数（Sigmoid）：

向量化批量计算

输入数据矩阵

将个样本堆叠为矩阵：

并行计算所有和

线性部分：

Python实现：

1	Z = np.dot(w.T, X) + b # 向量化实现

激活部分：

矩阵维度说明

的维度：
广播机制：标量会自动加到的每个元素上。
是样本矩阵，每列一个样本。
是行向量，包含所有样本的线性输出。

优势

效率提升：避免显式循环，利用NumPy的并行计算加速。
代码简洁性：一行代码完成全部样本的计算。

向量化 logistic 回归的梯度输出（Vectorizing Logistic Regression’s Gradient）

本节中大写字母代表向量，小写字母代表元素

对个训练数据做同样的运算，我们可以定义一个新的变量

我们已经去掉了一个for循环，我们的目标是不使用for循环，而是向量，我们可以这么做：

${dw = \frac{1}{m}Xdz^{T}\ }$

现在我们利用前五个公式完成了前向和后向传播，也实现了对所有训练样本进行预测和求导，再利用后两个公式，梯度下降更新参数，所以我们就通过一次迭代实现一次梯度下降，但如果希望多次迭代进行梯度下降，那么仍然需要for循环，放在最外层。

Python 中的广播（Broadcasting in Python）

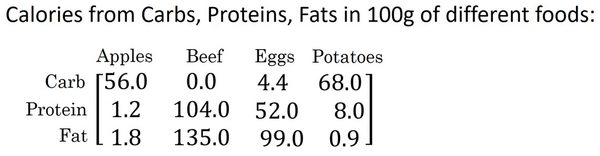
不同食物(C:/Users/15993/Desktop/深度学习笔记/image-20250327113144783.png)中不同营养成分的卡路里含量表格

这是一个不同食物(每100g)中不同营养成分的卡路里含量表格，表格为3行4列，列表示不同的食物种类，从左至右依次为苹果，牛肉，鸡蛋，土豆。行表示不同的营养成分，从上到下依次为碳水化合物，蛋白质，脂肪。

那么，我们现在想要计算不同食物中不同营养成分中的卡路里百分比。

import numpy as np
A = np.array([[56.0, 0.0, 4.4, 68.0],
              [1.2, 104.0, 52.0, 8.0],
              [1.8, 135.0, 99.0, 0.9]])
print(A)

输出：

1
2
3

[[ 56.    0.    4.4  68. ]
 [  1.2 104.   52.    8. ]
 [  1.8 135.   99.    0.9]]

按列求和（计算每列总和）

1 2	cal = A.sum(axis=0) # axis=0表示沿列方向求和 print(cal)

输出：

1	[ 59. 239. 155.4 76.9]

计算百分比（归一化每列）

1 2	percentage = 100 * A / cal.reshape(1, 4) # reshape确保广播正确 print(percentage)

输出：

1
2
3

[[94.91525424  0.          2.83140283 88.42652796]
 [ 2.03389831 43.51464435 33.46203346 10.40312094]
 [ 3.05084746 56.48535565 63.70656371  1.17035111]]

关键说明

A.sum(axis = 0)中的参数axis。axis用来指明将要进行的运算是沿着哪个轴执行，在numpy中，0轴是垂直的，也就是列，而1轴是水平的，也就是行。
而第二个A/cal.reshape(1,4)指令则调用了numpy中的广播机制。这里使用的矩阵除以的矩阵。技术上来讲，其实并不需要再将矩阵 reshape(重塑)成，因为矩阵本身已经是了。但是当我们写代码时不确定矩阵维度的时候，通常会对矩阵进行重塑来确保得到我们想要的列向量或行向量。重塑操作reshape是一个常量时间的操作，时间复杂度是，它的调用代价极低。

广播的例子

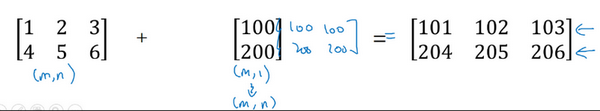
Broadcast Example

这里相当于是一个的矩阵加上一个的矩阵。在进行运算时，会先将矩阵水平复制次，变成一个的矩阵，然后再执行逐元素加法。

广播机制原则

numpy广播机制

如果两个数组的后缘维度的轴长度相符或其中一方的轴长度为1，则认为它们是广播兼容的。广播会在缺失维度和轴长度为1的维度上进行。

后缘维度的轴长度：A.shape[-1] 即矩阵维度元组中的最后一个位置的值

对于视频中卡路里计算的例子，矩阵后缘维度的轴长度是4，而矩阵的后缘维度也是4，则他们满足后缘维度轴长度相符，可以进行广播。广播会在轴长度为1的维度进行，轴长度为1的维度对应axis=0，即垂直方向，矩阵 $${cal}{1,4}$$ 沿axis=0(垂直方向)复制成为 ${cal{temp}}_{3,4}$ ，之后两者进行逐元素除法运算。

Broadcast Principle

矩阵和矩阵进行四则运算，后缘维度轴长度相符，可以广播，广播沿着轴长度为1的轴进行，即广播成为，之后做逐元素四则运算。

矩阵和矩阵进行四则运算，后缘维度轴长度不相符，但其中一方轴长度为1，可以广播，广播沿着轴长度为1的轴进行，即广播成为，之后做逐元素四则运算。

矩阵和常数进行四则运算，后缘维度轴长度不相符，但其中一方轴长度为1，可以广播，广播沿着缺失维度和轴长度为1的轴进行，缺失维度就是axis=0,轴长度为1的轴是axis=1，即广播成为，之后做逐元素四则运算。

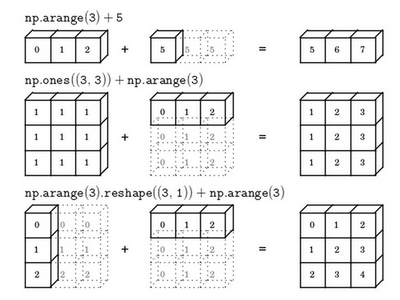
broadcast summary

关于 python _ numpy 向量的说明（A note on python or numpy vectors）

一维数组的陷阱

import numpy as np
a = np.random.randn(5)

print(a)
# Output:
# [ 0.5029632  -0.29691149  0.95429604 -0.82126861 -1.46269164]

print(a.shape)
# Output:
# (5,)

print(a.T)
# Output:
# [ 0.5029632  -0.29691149  0.95429604 -0.82126861 -1.46269164]

print(np.dot(a, a.T))
# Output:
# 4.0657109321

，这样会生成存储在数组中的5个高斯随机数变量。之后输出，此时的shape（形状）是一个的结构。这在Python中被称作一个一维数组。它既不是一个行向量也不是一个列向量。

print(a.T)
# Output:
# [ 0.5029632  -0.29691149  0.95429604 -0.82126861 -1.46269164]

print(np.dot(a, a.T))
# Output:
# 4.0657109321

a = np.random.randn(5,1)
print(a)
# Output:
# [[-0.0967311 ]
#  [-2.38617377]
#  [-0.3243588 ]
#  [-0.96216349]
#  [ 0.54410384]]

print(a.T)
# Output:
# [[-0.0967311  -2.38617377 -0.3243588  -0.96216349  0.54410384]]

编写神经网络时，不要使用shape为 (5,)、(n,) 或者其他一维数组的数据结构。相反，如果你设置为，那么这就将置于5行1列向量中。在先前的操作里和的转置看起来一样，而现在这样的变成一个新的的转置，并且它是一个行向量。请注意一个细微的差别，在这种数据结构中，当我们输出的转置时有两对方括号，而之前只有一对方括号，所以这就是1行5列的矩阵和一维数组的差别。

所以，不要使用

还有一件经常做的事，那就是如果我不完全确定一个向量的维度(dimension)，我经常会扔进一个断言语句(assertion statement)。像这样：

a = np.random.randn(5, 1)
# a.shape = (5, 1) → Column vector

a = np.random.randn(1, 5)
# a.shape = (1, 5) → Row vector

去确保在这种情况下是一个向量，或者说是一个列向量。这些断言语句实际上是要去执行的，并且它们也会有助于为你的代码提供信息。所以不论你要做什么，不要犹豫直接插入断言语句。如果你不小心以一维数组来执行，你也能够重新改变数组维数，表明一个数组或者一个数组：

1	assert(a.shape == (5,1))

不要使用一维数组,总是使用维矩阵（基本上是列向量），或者维矩阵（基本上是行向量），这样你可以减少很多assert语句来节省核矩阵和数组的维数的时间。另外，为了确保你的矩阵或向量所需要的维数时，不要羞于 reshape 操作。

一维数组的陷阱与最佳实践(这里是ai总结的本节笔记，用于对比看看哪个更清晰，使用Qwen2.5-Max)

在使用 NumPy 编写神经网络或进行矩阵运算时，正确处理数组的维度是非常重要的。如果不小心使用了一维数组（shape 为 (n,)），可能会导致一些不易察觉的错误和计算问题。以下是对常见陷阱的总结以及如何避免它们的最佳实践。

一维数组的问题

形状模糊
使用 a = np.random.randn(5) 创建的一维数组，其 shape 为 (5,)，既不是行向量也不是列向量。这种数组的行为在某些操作中可能会让人困惑。例如：
1
2
3
a = np.random.randn(5)
print(a.shape) # Output: (5,)
print(a.T) # Output: [ ... ] （转置后仍然是相同的一维数组）
点积结果不符合预期
如果你对两个一维数组进行点积（np.dot(a, a.T)），结果会是一个标量值（内积）。这可能不是你想要的结果，尤其是当你期望一个矩阵乘法时：
1
print(np.dot(a, a.T)) # Output: 标量值（如 4.0657109321）
缺乏明确的方向性
一维数组没有明确的“方向”（行或列），这可能导致后续操作中的维度不匹配问题。例如，矩阵乘法需要明确的行向量或列向量。

总结

不要使用一维数组 ((n,))，始终使用明确的二维数组（列向量 (n, 1) 或行向量 (1, n)）。
使用断言语句 验证数组的维度，确保它们符合预期。
使用 reshape 或 [:, None] 将一维数组转换为二维数组。
注意转置操作 的影响，确保矩阵运算的行为符合预期。

通过遵循这些最佳实践，你可以避免许多潜在的维度错误，并使代码更加清晰和健壮。

最终建议：始终以二维数组的形式处理数据，明确方向性和维度，减少调试时间并提高代码可靠性。

Boxed Final Recommendation:
$始终使用二维数组（列向量或行向量），并验证维度以确保正确性。$

3 浅层神经网络(Shallow neural networks)

3.1 神经网络概述（Neural Network Overview）

首先你需要输入特征，参数和，通过这些你就可以计算出：
$Missing or unrecognized delimiter for \right \left. \begin{array}{l} x\ w\ b \end{array} \right} \implies{z={w}^Tx+b} \implies{a = \sigma(z)}\ \implies{L}(a,y)$

接下来使用就可以计算出。我们将的符号换为表示输出,然后可以计算出loss function

Neural Network

在这个神经网络对应的3个节点，首先计算第一层网络中的各个节点相关的数，接着计算，在计算下一层网络同理；
我们会使用符号表示第层网络中节点相关的数，这些节点的集合被称为第层网络。

整个计算过程如下:
$Missing or unrecognized delimiter for \right \left. \begin{array}{r} {x }\ {W^{[1]}}\ {b^{[1]}} \end{array} \right} \implies{z^{[1]}=W^{[1]}x+b^{[1]}} \implies{a^{[1]} = \sigma(z^{[1]})}$

$Missing or unrecognized delimiter for \right \left. \begin{array}{r} \text{$a^{[1]} = \sigma(z^{[1]})$}\ \text{$W^{[2]}$}\ \text{$b^{[2]}$}\ \end{array} \right} \implies{z^{[2]}=W^{[2]}a^{[1]}+b^{[2]}} \implies{a^{[2]} = \sigma(z^{[2]})}\ \implies{L}\left(a^{[2]},y \right)$

类似逻辑回归，在计算后需要使用计算，接下来你需要使用另外一个线性方程对应的参数计算，
计算，此时就是整个神经网络最终的输出，用表示网络的输出。

在神经网络中我们也有从后向前的计算，最后会计算、，计算出来之后，然后计算计算、等
$Missing or unrecognized delimiter for \right \left. \begin{array}{r} {da^{[1]} = {d}\sigma(z^{[1]})}\ {dW^{[2]}}\ {db^{[2]}}\ \end{array} \right} \impliedby{dz}^{[2]}={d}(W^{[2]}\alpha^{[1]}+b^{[2]}) \impliedby{da}^{[2]} = {d}\sigma(z^{[2]})\ \impliedby{dL}\left(a^{[2]},y \right)$

3.2 神经网络的表示（Neural Network Representation）

A Neural Network

记号可以用来表示输入特征。表示激活（activate）的意思，它意味着网络中不同层的值会传递到它们后面的层中。隐藏层也同样会产生一些激活值，那么我将其记作，所以具体地，这里的第一个单元或结点我们将其表示为$a^{[1]}{1} $，第二个结点的值我们记为$ a^{[1]}{2} $。最后输出层将产生某个数值$ a $，它只是一个单独的实数，所以的$ \hat{y} $值将取为$ a^{[2]}$。

这是一个两层的神经网络，因为我们计算网络的层数时，输入层是不算入总层数内，所以隐藏层是第一层，输出层是第二层。

隐藏层以及最后的输出层是带有参数的，这里的隐藏层将拥有两个参数和，将给它们加上上标(,)，表示这些参数是和第一层这个隐藏层有关系的。之后在这个例子中我们会看到是一个4x3的矩阵，而是一个4x1的向量，第一个数字4源自于我们有四个结点或隐藏层单元，然后数字3源自于这里有三个输入特征。相似的输出层也有一些与之关联的参数以及。从维数上来看，它们的规模分别是1x4以及1x1。1x4是因为隐藏层有四个隐藏层单元而输出层只有一个单元。

Note of Neural Network Representation

3.3 计算一个神经网络的输出（Computing a Neural Network’s output）

3.3.1 神经网络的计算

NN Unit

首先按步骤计算出，然后在第二步中以sigmoid函数为激活函数计算（得出），一个神经网络只是这样子做了好多次重复计算。

针对上面的两层的神经网络：

第一步，计算。

第二步，通过激活函数计算。

隐藏层的第二个以及后面两个神经元的计算过程一样，只是注意符号表示不同，最终分别得到 $、、$ ，详细结果见下:

3.3.2 向量化计算

2 Layer NN Cauculation

向量化的过程是将神经网络中的一层神经元参数纵向堆积起来，例如隐藏层中的纵向堆积起来变成一个的矩阵，用符号表示。另一个看待这个的方法是我们有四个逻辑回归单元，且每一个逻辑回归单元都有相对应的参数——向量，把这四个向量堆积在一起，你会得出这4×3的矩阵。
因此，
公式3.8：

公式3.9：

详细过程见下:
公式3.10：
$$
a^{[1]} =
\left[
\begin{array}{c}
a^{[1]}{1}\
a^{[1]}{2}\
a^{[1]}{3}\
a^{[1]}{4}
\end{array}
\right]
= \sigma(z^{[1]})
$公式：$
\left[
\begin{array}{c}
z^{[1]}{1}\
z^{[1]}{2}\
z^{[1]}{3}\
z^{[1]}{4}\
\end{array}
\right]
=
\overbrace{
\left[
\begin{array}{c}
…W^{[1]T}{1}…\
…W^{[1]T}{2}…\
…W^{[1]T}{3}…\
…W^{[1]T}{4}…
\end{array}
\right]
}^{W^{[1]}}
*
\overbrace{
\left[

\right]
}^{input}
+
\overbrace{
\left[

\right]
}^{b^{[1]}}
$$

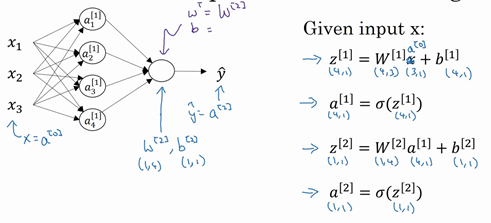
对于神经网络的第一层，给予一个输入，得到，可以表示为。通过相似的衍生你会发现，后一层的表示同样可以写成类似的形式，得到，，具体过程见公式3.8、3.9。

如上图左半部分所示为神经网络，把网络左边部分盖住先忽略，那么最后的输出单元就相当于一个逻辑回归的计算单元。当你有一个包含一层隐藏层的神经网络，你需要去实现以计算得到输出的是右边的四个等式，并且可以看成是一个向量化的计算过程，计算出隐藏层的四个逻辑回归单元和整个隐藏层的输出结果，如果编程实现需要的也只是这四行代码。

3.4 多样本向量化（Vectorizing across multiple examples）

3.4.1 多样本的神经网络计算

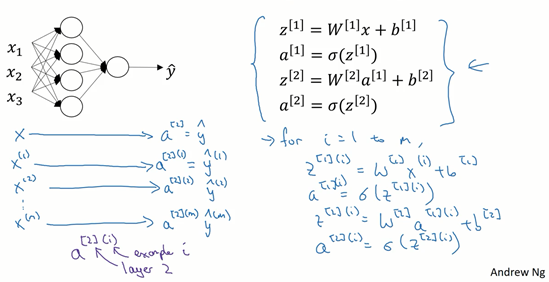
Example

逻辑回归是将各个训练样本组合成矩阵，对矩阵的各列进行计算。神经网络是通过对逻辑回归中的等式简单的变形，让神经网络计算出输出值。这种计算是所有的训练样本同时进行的。

用第一个训练样本来计算出预测值，就是第一个训练样本上得出的结果。

然后，用来计算出预测值，循环往复，直至用计算出。

用激活函数表示法，如上图左下所示，它写成$a^{2} $、$ a^{2} $和$ a^{2}$。

$a^{2} $，$ (i) $是指第$ i $个训练样本而$ [2]$是指第二层

3.4.2 向量化多样本神经网络计算

Vectorizing across multiple examples

如果采用非向量化的实现，我们就需要使用for循环遍历每一个训练样本（左上角），所以接下来我们要让这个过程向量化。

定义向量等于训练样本，将它们组合成矩阵的各列，形成一个维或维矩阵。以此类推，从小写的向量到这个大写的矩阵，只是通过组合向量在矩阵的各列中：

同理，$z^{1} $，$ z^{1} $等等都是$ z^{1} $的列向量，将所有$ m $都组合在各列中，就的到矩阵$ Z^{[1]} $：$ $
Z^{[1]} =
\left[
\begin{array}{c}
\vdots & \vdots & \vdots & \vdots\
z^{1} & z^{1} & \cdots & z^{1}\
\vdots & \vdots & \vdots & \vdots\
\end{array}
\right]
$$

同理，$a^{1} $，$ a^{1} $，，$ a^{1} $将其组合在矩阵各列中，如同从向量$ x $到矩阵$ X $，以及从向量$ z $到矩阵$ Z $一样，就能得到矩阵$ A^{[1]} $：$ $
A^{[1]} =
\left[
\begin{array}{c}
\vdots & \vdots & \vdots & \vdots\
\alpha^{1} & \alpha^{1} & \cdots & \alpha^{1}\
\vdots & \vdots & \vdots & \vdots\
\end{array}
\right]
$同样的，对于和，也是这样得到：$
\left.
\begin{array}{r}
\text{$z^{1} = W^{1}x^{(i)} + b^{[1]}$}\
\text{$\alpha^{1} = \sigma(z^{1})$}\
\text{$z^{2} = W^{2}\alpha^{1} + b^{[2]}$}\
\text{$\alpha^{2} = \sigma(z^{2}) $Extra close brace or missing open brace}\ \end{array} \right} \implies \begin{cases} \text{$A^{[1]} = \sigma(z^{[1]})$}\ \text{$z^{[2]} = W^{[2]}A^{[1]} + b^{[2]}$}\ \text{$A^{[2]} = \sigma(z^{[2]})$}\ \end{cases}$ $

这种符号其中一个作用就是，可以通过训练样本来进行索引。这就是水平索引对应于不同的训练样本的原因，这些训练样本是从左到右扫描训练集而得到的。

在垂直方向，这个垂直索引对应于神经网络中的不同节点。例如，这个节点，该值位于矩阵的最左上角对应于激活单元，它是位于第一个训练样本上的第一个隐藏单元。它的下一个值对应于第二个隐藏单元的激活值。它是位于第一个训练样本上的，以及第一个训练示例中第三个隐藏单元，等等。

当垂直扫描，是索引到隐藏单位的数字。当水平扫描，将从第一个训练示例中从第一个隐藏的单元到第二个训练样本，第三个训练样本……直到节点对应于第一个隐藏单元的激活值，且这个隐藏单元是位于这个训练样本中的最终训练样本。

从水平上看，矩阵代表了各个训练样本。从竖直上看，矩阵的不同的索引对应于不同的隐藏单元。

对于矩阵 $，$ 情况也类似，水平方向上，对应于不同的训练样本；竖直方向上，对应不同的输入特征，而这就是神经网络输入层中各个节点。

神经网络上通过在多样本情况下的向量化来使用这些等式。

3.5 向量化实现的解释（Justification for vectorized implementation）

3.5.1 向量化实现的解释

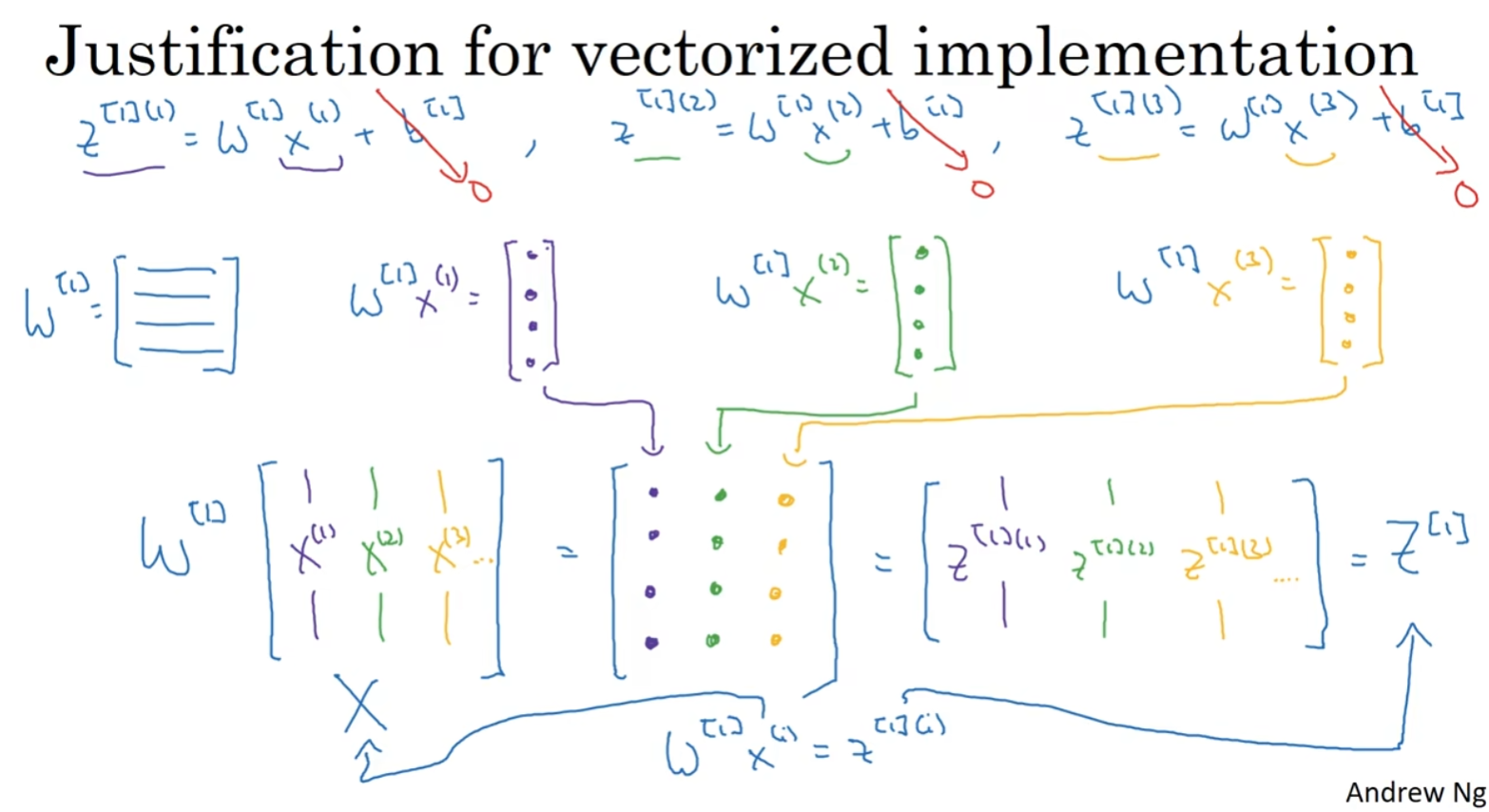
Justification for vectorized implementation

现在是一个矩阵，都是列向量，矩阵乘以列向量得到列向量，下面将它们用图形直观的表示出来:
$$
W^{[1]} x =
\left[

\right]

    \left[
    \begin{array}{c}
    \vdots &\vdots & \vdots & \vdots \\
    x^{(1)} & x^{(2)} & x^{(3)} & \vdots\\
    \vdots &\vdots & \vdots & \vdots \\
    \end{array}
    \right]
    =
    \left[
    \begin{array}{c}
    \vdots &\vdots & \vdots & \vdots \\
    w^{(1)}x^{(1)} & w^{(1)}x^{(2)} & w^{(1)}x^{(3)} & \vdots\\
    \vdots &\vdots & \vdots & \vdots \\
    \end{array}
    \right]
    =\\
    \left[
    \begin{array}{c}
    \vdots &\vdots & \vdots & \vdots \\
    z^{[1](1)} & z^{[1](2)} & z^{[1](3)} & \vdots\\
    \vdots &\vdots & \vdots & \vdots \\
    \end{array}
    \right]
    =
    Z^{[1]}

从图中可以看出，当加入更多样本时，只需向矩阵中加入更多列。

所以从这里我们也可以了解到，为什么之前我们对单个样本的计算要写成
$z^{1} = W^{[1]}x^{(i)} + b^{[1]} $这种形式，因为当有不同的训练样本时，将它们堆到矩阵$ X $的各列中，那么它们的输出也就会相应的堆叠到矩阵$ Z^{[1]}$ 的各列中。

Recap

实际上可以记为，使用同样的方法就可以由神经网络中的每一层的输入计算输出。其实这些方程有一定对称性，其中第一个方程也可以写成，这对方程形式其实很类似，只不过这里所有指标加了1。所以这样就显示出神经网络的不同层次，大概每一步做的都是一样的，随着网络的深度变大，基本上也还是重复这两步运算，只不过是比这里你看到的重复次数更多。

3.5.2 向量化总结

其实从第二章和第三章中讲向量化的过程就可以发现了，向量化最重要的事情就在于将for循环中的每个向量直接堆叠成矩阵，并通过矩阵计算的方式消除掉for循环但是得到一样的输出结果。

3.6 激活函数（Activation functions）

3.6.1 常见的激活函数

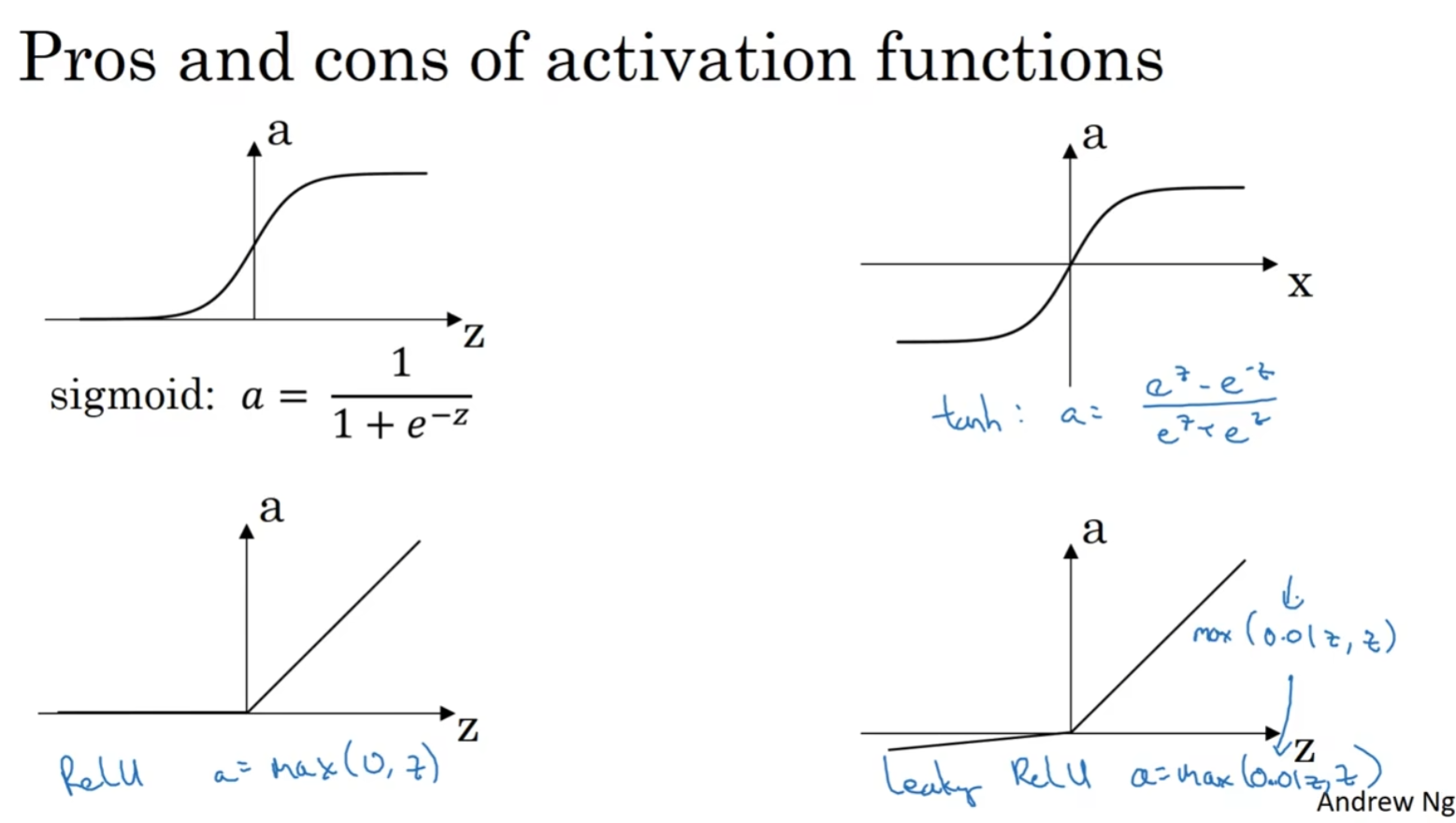
Pros and cons of activation fuctions

sigmoid函数：

tanh函数:

tanh函数是sigmoid的向下平移和伸缩后的结果。对它进行了变形后，穿过了点，并且值域介于+1和-1之间。

事实证明，如果在隐藏层上使用函数效果总是优于sigmoid函数。因为函数值域在-1和+1的激活函数，其均值是更接近零均值的。在训练一个算法模型时，如果使用tanh函数代替sigmoid函数中心化数据，使得数据的平均值更接近0而不是0.5。

修正线性单元函数（ReLU）：

只要是正值的情况下，导数恒等于1，当是负值的时候，导数恒等于0。

Leaky ReLU：

当是负值时，这个函数的值不是等于0，而是轻微的倾斜。

ReLU和Leacky ReLU的优点：

第一，在的区间变动很大的情况下，激活函数的导数或者激活函数的斜率都会远大于0，在程序实现就是一个if-else语句，而sigmoid函数需要进行浮点四则运算，在实践中，使用ReLU激活函数神经网络通常会比使用sigmoid或者tanh激活函数学习的更快。

第二，sigmoid和tanh函数的导数在正负饱和区的梯度都会接近于0，这会造成梯度弥散，而ReLU和Leaky ReLU函数大于0部分都为常数，不会产生梯度弥散现象。(同时应该注意到的是，ReLU进入负半区的时候，梯度为0，神经元此时不会训练，产生所谓的稀疏性，而Leaky ReLU不会有这问题)

3.6.2 激活函数的选择

sigmoid激活函数：除了输出层是一个二分类问题基本不会用它。

tanh激活函数：tanh是非常优秀的，几乎适合所有场合。

ReLU激活函数：最常用的默认函数，如果不确定用哪个激活函数，就使用ReLU或者Leaky ReLU。

3.7 为什么需要非线性激活函数？（why need a nonlinear activation function?）

如果你是用线性激活函数或者叫恒等激励函数，那么神经网络只是把输入线性组合再输出（线性函数无论如何组合最终都是一个线性函数）。

不能在隐藏层用线性激活函数，可以用ReLU或者tanh或者leaky ReLU或者其他的非线性激活函数，唯一可以用线性激活函数的通常就是输出层；除了这种情况，会在隐层用线性函数的，除了一些特殊情况，比如与压缩有关的，否则几乎不可能。

3.8 激活函数的导数（Derivatives of activation functions）

1）sigmoid activation function

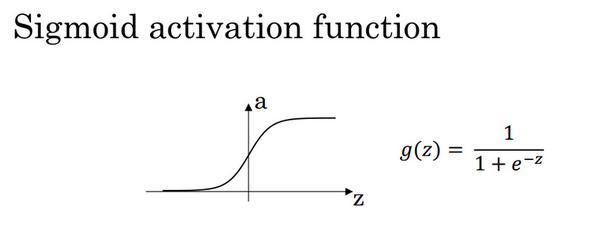
sigmoid

其具体的求导如下：

当 = 10或 ;

当= 0 ,

在神经网络中;

Tanh activation function

tanh

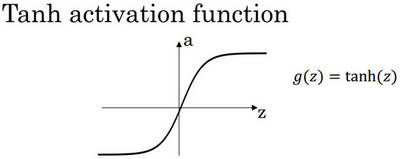
其具体的求导如下：

当 = 10或

当 = 0,

在神经网络中;

3）Rectified Linear Unit (ReLU)

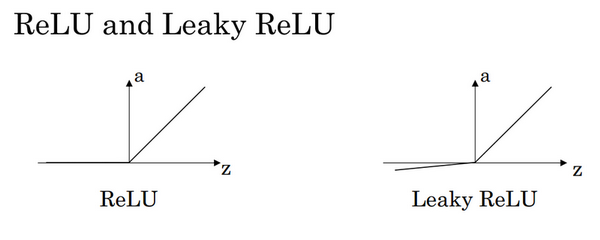
ReLU and Leaky ReLU

注：通常在= 0的时候给定其导数1或0；但是=0的情况很少

4）Leaky linear unit (Leaky ReLU)

与ReLU类似

注：通常在的时候给定其导数1或0.01；但是的情况很少。

3.9 神经网络的梯度下降（Gradient descent for neural networks）

正向传播方程如下：
forward propagation：

反向传播方程如下:

back propagation：

$ dz^{[1]} = \underbrace{W^{[2]T}{\rm d}z^{[2]}}{(n^{[1]},m)}\quad*\underbrace{g’^{[1]}}{activation ; function ; of ; hidden ; layer}*\quad\underbrace{(z^{[1]})}{(n^{[1]},m)} dW^{[1]} = {\frac{1}{m}}dz^{[1]}x^{T}{\underbrace{db^{[1]}}{(n^{[1]},1)}} = {\frac{1}{m}}np.sum(dz^{[1]},axis=1,keepdims=True)$

这些都是针对所有样本进行过向量化，是的矩阵；这里np.sum是python的numpy命令，axis=1表示水平相加求和，keepdims是防止python输出那些古怪的秩数，加上这个确保阵矩阵这个向量输出的维度为这样标准的形式。

还有一种防止python输出奇怪的秩数，需要显式地调用reshape把np.sum输出结果写成矩阵形式。

3.10（Math）直观理解反向传播（Backpropagation intuition）

3.10.1 Logistic Regression

回想一下逻辑回归的公式
$Missing or unrecognized delimiter for \right \left. \begin{array}{l} {x }\ {w }\ {b } \end{array} \right} \implies{z={w}^Tx+b} \implies{\alpha = \sigma(z)} \implies{L\left(a,y \right)}$
所以回想当时我们讨论逻辑回归的时候，我们有这个正向传播步骤，其中我们计算，然后，然后损失函数。

$$
\underbrace{
\left.

\right}
}{dw={dz}\cdot x, db =dz}
\impliedby\underbrace{z={w}^Tx+b}{dz=da\cdot g^{‘}(z),
g(z)=\sigma(z),
{\frac{dL}{dz}}={\frac{dL}{da}}\cdot{\frac{da}{dz}},
{\frac{d}{ dz}}g(z)=g^{‘}(z)}
\impliedby\underbrace{ {a = \sigma(z)}
\impliedby{L(a,y)}}_{da={\frac{d}{da}}{L}\left(a,y \right)=(-y\log{\alpha} - (1 - y)\log(1 - a))^{‘}={-\frac{y}{a}} + {\frac{1 - y}{1 - a}{}} }
$$

Logistic gradients

3.10.2 Neural Network

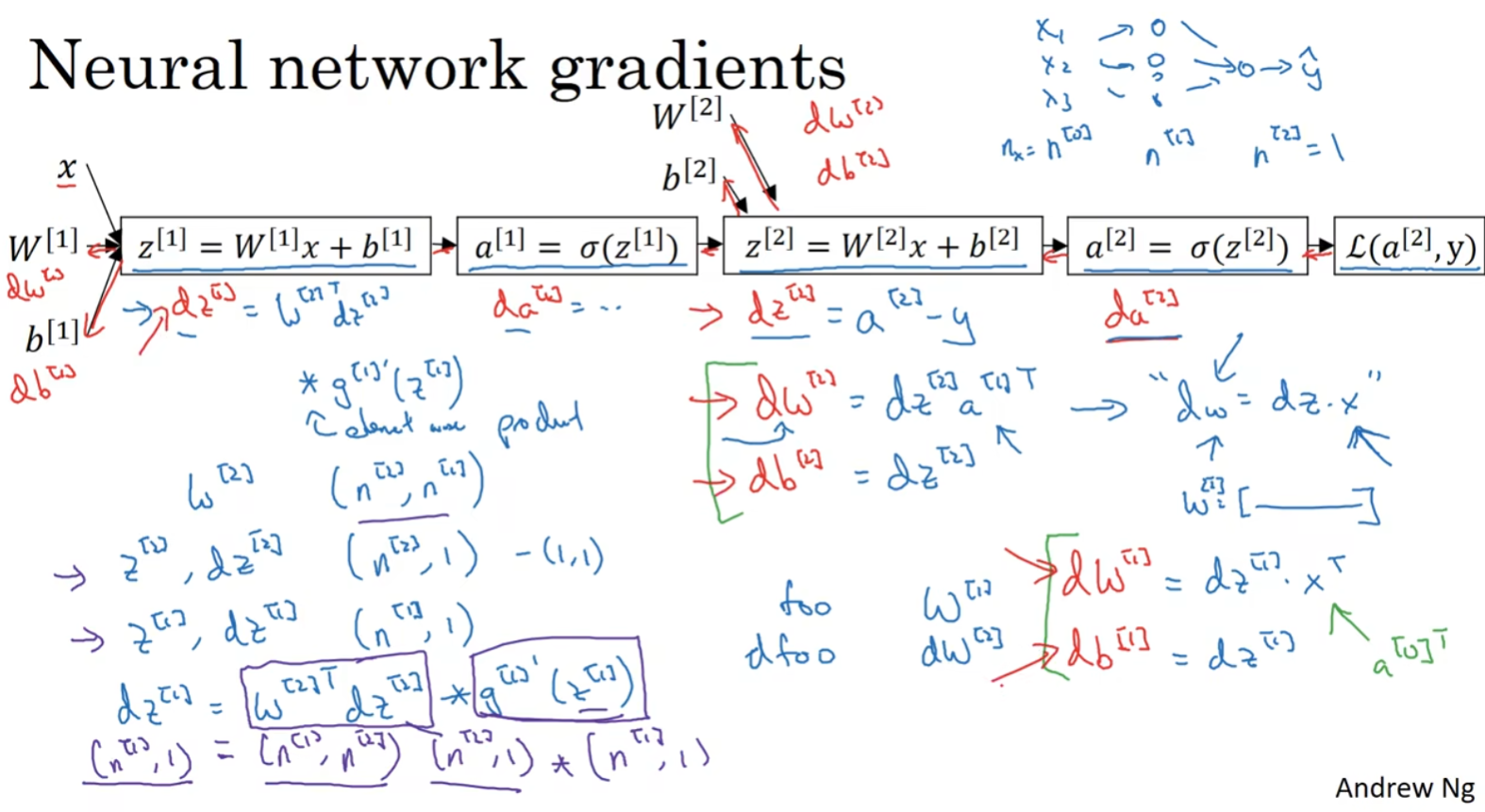
Neural Netork gradients

神经网络的计算中，与逻辑回归十分类似，但中间会有多层的计算。下图是一个双层神经网络，有一个输入层，一个隐藏层和一个输出层。

前向传播：

计算，，再计算，，最后得到loss function。

反向传播：

向后推算出，然后推算出，接着推算出，然后推算出。我们不需要对求导，因为是固定的，我们也不是想优化。向后推算出，然后推算出的步骤可以合为一步：
$，$
(注意：逻辑回归中；为什么多了个转置：中的(视频里是)是一个列向量，而是个行向量，故需要加个转置);
公式3.41：

公式3.42：

注意：这里的矩阵：的维度是：。

，的维度都是：，如果是二分类，那维度就是。

，的维度都是：。

证明过程：
见公式3.42，其中维度为：、相乘得到，和维度相同，

的维度为，这就变成了两个都是向量逐元素乘积。

实现后向传播有个技巧，就是要保证矩阵的维度相互匹配。最后得到和，公式3.43：

可以看出和非常相似，其中扮演了的角色，等同于。

由：

得到：

$$
Z^{[1]} =
\left[
\begin{array}{c}
\vdots &\vdots & \vdots & \vdots \
z^{1} & z^{1} & \vdots & z^{1} \
\vdots &\vdots & \vdots & \vdots \
\end{array}
\right]
$$
注意：大写的表示$z^{1},z^{1},z^{1}…z^{1}$的列向量堆叠成的矩阵，以下类同。

下图写了主要的推导过程：

Summary 公式3.44：
$，$
公式3.45：

公式3.46：

公式3.47：
$\underbrace{dZ^{[1]}}{(n^{[1]}, m)} = \underbrace{W^{[2]T}dZ^{[2]}}{(n^{[1]}, m)}*\underbrace{g[1]^{‘}(Z^{[1]})}_{(n^{[1]}, m)} $公式：$ dW^{[1]} = {\frac{1}{m}}dZ^{[1]}x^{T} $公式：$ db^{[1]} = {\frac{1}{m}}np.sum(dZ^{[1]},axis=1,keepdims=True) $

3.11 随机初始化（Random Initialization）

对于一个神经网络，如果你把权重或者参数都初始化为0，那么梯度下降将不会起作用。

3.11.1 举个栗子

有两个输入特征，，2个隐藏层单元就等于2。
因此与一个隐藏层相关的矩阵，或者说是2*2的矩阵，假设把它初始化为0的2*2矩阵，也等于，把偏置项初始化为0是合理的，但是把初始化为0就有问题了。
那这个问题如果按照这样初始化的话，你总是会发现和相等，这个激活单元和这个激活单元就会一样。因为两个隐含单元计算同样的函数，当你做反向传播计算时，这会导致$\text{dz}{1}^{[1]} $和$ \text{dz}{2}^{[1]} $也会一样，对称这些隐含单元会初始化得一样，这样输出的权值也会一模一样，由此$ W^{[2]} $等于$ [0;0]$；

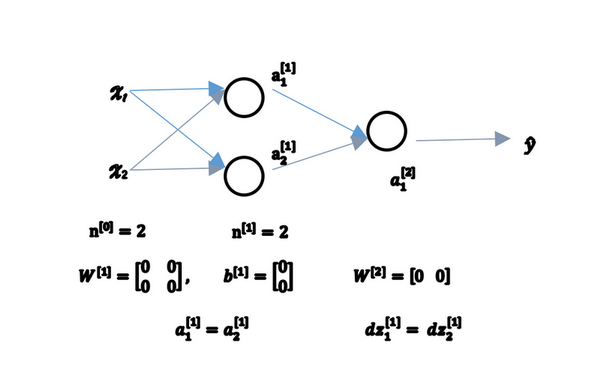
Example

图3.11.1
但是如果你这样初始化这个神经网络，那么这两个隐含单元就会完全一样，因此他们完全对称，也就意味着计算同样的函数，并且肯定的是最终经过每次训练的迭代，这两个隐含单元仍然是同一个函数，令人困惑。会是一个这样的矩阵，每一行有同样的值因此我们做权重更新把权重每次迭代后的，第一行等于第二行。

由此可以推导，如果你把权重都初始化为0，那么由于隐含单元开始计算同一个函数，所有的隐含单元就会对输出单元有同样的影响。一次迭代后同样的表达式结果仍然是相同的，即隐含单元仍是对称的。通过推导，两次、三次、无论多少次迭代，不管你训练网络多长时间，隐含单元仍然计算的是同样的函数。因此这种情况下超过1个隐含单元也没什么意义，因为他们计算同样的东西。当然更大的网络，比如你有3个特征，还有相当多的隐含单元。

3.11.2 随机初始化参数

把设为np.random.randn(2,2)(生成高斯分布)，通常再乘上一个小的数，比如0.01，这样把它初始化为很小的随机数。然后没有这个对称的问题（叫做symmetry breaking problem），所以可以把初始化为0，因为只要随机初始化你就有不同的隐含单元计算不同的东西，因此不会有symmetry breaking问题了。相似的，对于你可以随机初始化，可以初始化为0。

$W^{[1]} = np.random.randn(2,2);;0.01;,;b^{[1]} = np.zeros((2,1))W^{[2]} = np.random.randn(2,2);;0.01;,;b^{[2]} = 0$

PS：为什么是0.01嘞？

我们通常倾向于初始化为很小的随机数。因为如果你用tanh或者sigmoid激活函数，或者说只在输出层有一个Sigmoid，如果（数值）波动太大，当你计算激活值时如果很大，就会很大或者很小，因此这种情况下你很可能停在tanh/sigmoid函数的平坦的地方(见图3.8.2)，这些地方梯度很小也就意味着梯度下降会很慢，因此学习也就很慢。

如果很大，那么你很可能最终停在（甚至在训练刚刚开始的时候）很大的值，这会造成tanh/Sigmoid激活函数饱和在龟速的学习上，如果你没有sigmoid/tanh激活函数在你整个的神经网络里，就不成问题。但如果你做二分类并且你的输出单元是Sigmoid函数，那么你不会想让初始参数太大，因此这就是为什么乘上0.01或者其他一些小数是合理的尝试。对于一样，就是np.random.randn((1,2))，我猜会是乘以0.01。

深度学习笔记

神经网络和深度学习(Neural Networks and Deep Learning)

神经网络

监督学习

数据

深度学习兴起

神经网络的编程基础(Basics of Neural Network programming)

二分分类

一些符号

Logistic回归

Sigmoid函数

Sigmoid函数的图像

重要说明

逻辑回归的代价函数（Logistic Regression Cost Function）

逻辑回归成本函数

损失（误差）函数（单个样本）

成本函数（所有样本）

梯度下降法

梯度下降过程

Logistic Regression 中的梯度下降（Logistic Regression Gradient Descent）

前向传播

计算图表示

反向传播导数

参数梯度

参数更新规则

实例演示

关键理解

Logistic Regression on Examples

1. 成本函数（Cost Function）

2. 目标函数的梯度计算

2.1 对 的偏导

2.2 对 的偏导

3. 梯度下降算法实现（带循环）

3.1 前向传播

3.2 损失和梯度计算

3.3 最终平均值

4. 参数更新（梯度下降）

代码流程

向量化（Vectorization）

基本概念

数学表达

向量化实现

实例说明

优势总结

向量与矩阵值函数的逐元素运算

基本概念

Python实现示例

手动循环实现

使用NumPy内置函数

逐元素运算的数学性质

应用场景

向量化的示例应用

广播机制（Broadcasting）

向量化的梯度计算

避免常见错误

实际案例：逻辑回归

性能对比

向量化逻辑回归的实现

单样本计算基础

向量化批量计算

输入数据矩阵

并行计算所有 和

矩阵维度说明

优势

向量化 logistic 回归的梯度输出（Vectorizing Logistic Regression’s Gradient）

Python 中的广播（Broadcasting in Python）

按列求和（计算每列总和）

计算百分比（归一化每列）

关键说明

广播的例子

广播机制原则

关于 python _ numpy 向量的说明（A note on python or numpy vectors）

一维数组的陷阱

一维数组的陷阱与最佳实践(这里是ai总结的本节笔记，用于对比看看哪个更清晰，使用Qwen2.5-Max)

一维数组的问题

推荐的最佳实践

1. 明确使用二维数组

2. 使用断言语句验证维度

3. 使用 reshape 调整维度

4. 注意转置操作

2.1 对的偏导

2.2 对的偏导

并行计算所有和

3. 使用 `reshape` 调整维度