深度学习笔记

AFLGo基本原理

AFLGo的流程架构

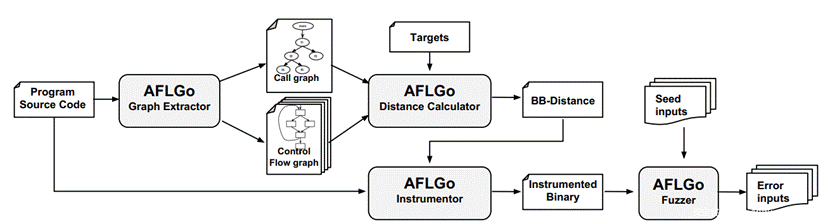
1.首先，编译源码，得到待 fuzz 程序的控制流图 (Control Flow Graph, CFG) 和函数调用图 (Call Graph, CG) 。

2.其次，通过 CFG 和 CG，以及给定的 target，计算所有的基本块 (Basic Block, BB) 到 target 所在的基本块的距离。这一步由 python 脚本完成。

3.然后，再编译一次源码，对程序进行插桩，除了AFL原有的插桩逻辑外，添加向指定地址增加每个基本块距离的指令，即指定一个共享内存地址为记录 distance 的变量，在基本块中插桩，插入如下指令：distance += current_BB_distance，向 distance 变量增加当前基本块的距离。

4.最后是 fuzzing 部分的逻辑，根据插桩反馈的信息，我们可以在每一个 seed 作为输入给程序执行的时候得到这个 seed 对应的 distance，也就是 seed 执行路径距离目标点的距离，然后根据距离对 seed 进行打分，这个打分的算法就是模拟退火算法，距离越近，打分越高，seed 得到变异的机会越多。

至此，整个 AFLGo 的流程结束。

Aflgo距离计算模块

AFLGO 首先根据 函数调用图CG 计算函数层面的距离，然后基于 CFG 计算基本块层面的距离，最后将基本块的距离作为插桩时使用的距离。

因为 AFLGo 支持标记多个目标，所以在距离计算时需要将每个基本块到多个目标的距离做一个加和，这里采用的是对到每个目标的距离和取调和平均数。

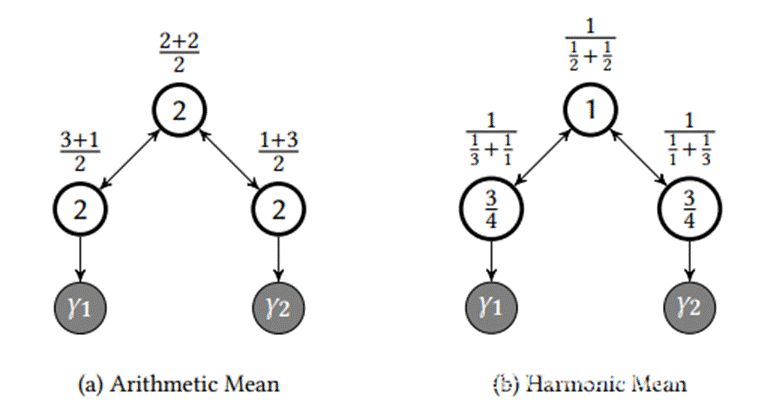
为什么不取算术平均数？因为在多目标的情况下，算术平均数无法区分『一个基本块离一个目标近一个目标远』和『一个基本块离两个目标点距离相等』的情况。

如下图，当目标为Y1和Y2时，三个白色基本块都可以到达这两个灰色的目标点。当用算术平均数计算时，左右分别到两个目标点的距离是1和3，平均下来就是(1+3) / 2= 2。而最上面的点到两个目标的距离都是2，平均下来也是2，这样三个点距离都是2，区分不出到哪个点距离近。如果取调和平均数，左右两个点距离都是是3/4，最上面的点距离是1，这样就能区分出远近了。

函数层面距离计算

目标基本块所在的函数就是目标函数。

公式看起来比较复杂，其实就是两句话：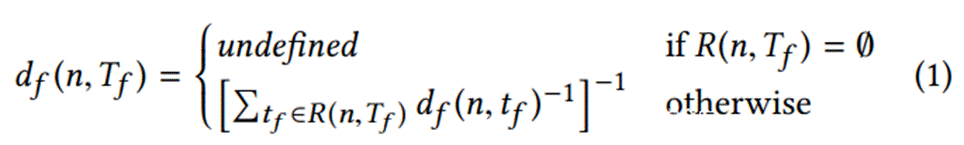

1.当该函数不能到达任意一个目标函数(即：CG上该函数没有路径能到达目标函数)时，不定义距离

2.否则，将该函数能够到达的目标函数之间的最短距离取调和平均数

基本块层面距离计算

有了函数层面的距离，再计算更加细的基本块距离，规则如下：

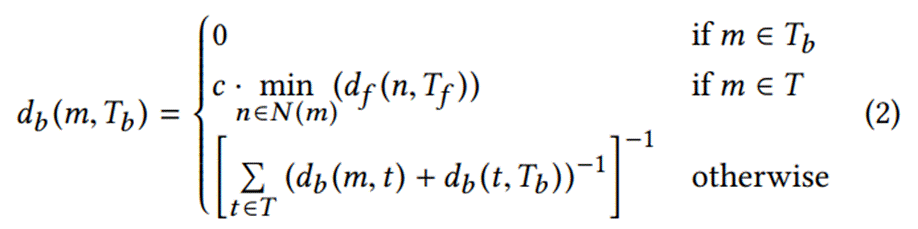
1.当基本块就是目标基本块时，该基本块的距离为0

2.当当前基本块存在函数调用链可以到达目标函数时，距离为该基本块调用的函数集和中，『距离目标函数最近的路径距离』乘上一个系数

3.否则，距离为『有能到达目标基本块的后继基本块时，取当前基本块到后继基本块距离』 + 『该后继基本块到目标基本块的距离』，取到所有目标的调和平均数

模拟退火算法

模拟退火算法是为了解决探索-利用 (exploration-exploitation)的问题。

在fuzzing的前期，因为探索到的路径有限，此时离目标点的距离可能还很远，此时重点在探索，即尽可能扩大覆盖率，当覆盖率到一定程度时，再利用距离较近的seed来变异，此时到达目标点的可能性更大。

如果在距离还很远的时候，就只针对当前距离最近的seed进行变异，虽然当前seed距离是相对最近的，但是在绝对距离上可能还很远，无论怎么fuzzing，到达目标点的可能性就很小，这样就可能会陷入局部最优的困境中。

模拟退火算法就是为了避免fuzzing陷入局部最优的困境中的方法。

AFL中有一个环节叫 power scheduling，即对 seed 进行打分，综合各项指标计算分数，这个分数直接影响到对每个 seed 进行 fuzzing 的时间长度。

而 AFLGo 在 power scheduling 部分加上模拟退火算法，同时以时间和距离来计算分数。当时间越长，距离越近的 seed 得分越高，能够得到 fuzzing 的时间越长。

多脆弱点挖掘技术

技术1：

参考论文：

Constraint-guided Directed Greybox Fuzzing | USENIX

约束导向的定向灰盒模糊测试

该项目代码不开源

约束引导定向灰盒模糊(CDGF)旨在按顺序满足一系列约束，而传统的DGF仅旨在达到一组独立的目标位点。每个约束都有自己需要达到的目标站点，以及需要在其目标站点上满足的数据条件。

为了实现这一目标，CDFG对更有可能满足所有约束的种子进行模糊处理。换句话说，对于以下两种情况，它给出了更短的种子距离:1)如果它满足更多的约束，2)如果它比另一个更接近于满足第一个未满足的约束

CDGF通过组合每个约束的距离来定义约束序列的距离或总距离。当前面的约束不满足时，CDGF认为单个约束的距离达到最大值，当剩下更多的约束不满足时，CDGF得到的总距离更长。

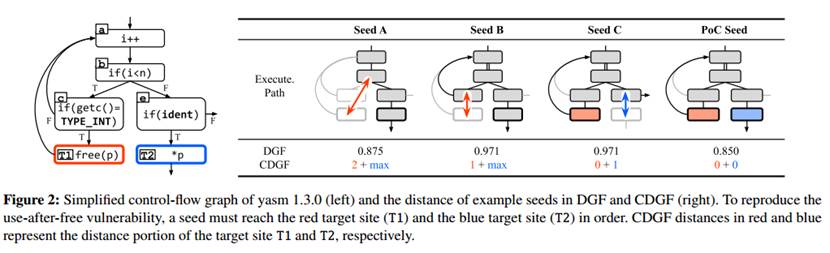
约束指示程序首先到达T1，在那里内存对象被释放，然后到达T2，在那里释放的内存对象被使用。给定图2中的种子和图4中的约束条件，CDGF计算种子的距离如下:

• Seed A.因为它在距离T1两个块的b处最接近T1，所以第一个约束的距离是2。同时，由于未能到达T1，第一个约束%free的目标位点，所以无论是否到达T2，第二个约束%use的距离都是最大的。将两个距离结合起来，种子距离计算为2+max。

• Seed B.因为它接近T1的距离更近，因为它接触到距离T1一个块c，所以T1的距离是1。同时%use距离仍然是最大的，因为它在到达T2之前仍然没有到达T1。结合两者，种子距离计算为1+max。

• Seed C.因为它在T2之前到达T1，所以%free的距离为0。同时，由于它在e处使T2偏转了一个基本块，所以%use的距离为1。两者结合，种子距离为1。

通过对距离较短的种子进行优先排序，CDGF可以在更理想的种子基础上变异种子，并快速触发崩溃。

技术2：

参考论文：Titan: Efficient Multi-target Directed Greybox Fuzzing (computer.org)

开源链接：5hadowblad3/Titan: Research artifact for Oakland (S&P) 2024, “Titan: Efficient Multi-target Directed Greybox Fuzzing” (github.com)

现有的模糊测试不知道目标靶点之间的相关性，因此，随着目标靶点数量的增加，可能会退化为无向模糊。最终，模糊器不能有效地选择种子并有效地生成多个目标的输入，称之为协同无知问题。

针对此问题

1. 设计了一个精确的静态分析来推断达到多个测试目标的协同作用，使我们能够通过区分目标之间的相关性来减轻协同忽略问题。
2. 协同感知调度策略，该策略通过种子的细粒度排序来发现种子可能到达的目标最多。
3. 以多目标为导向的突变，生成接近多个目标的输入，所需的执行次数更少。

静态分析：给定一组目标程序点，设计了两步静态分析:推断达到每个目标的先决条件、计算区分多个目标的相关性。

先决条件分析：

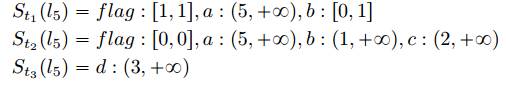
计算多个目标相关性：

不同目标的推断变量范围可能具有许多相关性。例如，考虑上面示例中的多目标可达性摘要。达到目标1和目标2都要求变量a的范围相同，但它们对变量b的范围有排他性要求。

计算公式

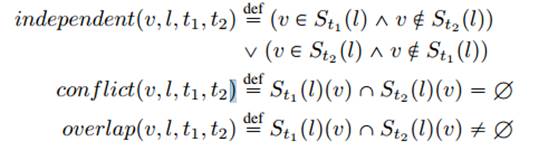
协同感知种子调度：

确定种子可到达的靶点：

种子应该关注条件较满足的目标，而不是同时解决所有目标的条件。因此，不是所有的目标都应该被种子考虑。由于冲突相关性表示两个目标的矛盾，因此在调度过程中，我们认为其中一个目标与当前种子无关。

确定种子到达靶点的潜力：

使用在执行中满足的先决条件的比例来度量一个种子( 记为potential（t）)

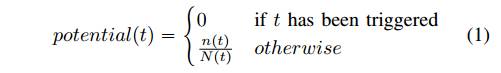
有了到达每个靶点的潜力，我们将它们累积为一个种子s来衡量达到这些靶点的可能性

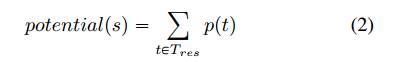
以多目标为导向的突变：

为了有效地生成多个目标的输入，我们提出同时对不同目标的多个字节进行变异。具体来说，我们首先推断影响不同目标的字节，以确定哪些可以同时突变。然后我们优先改变那些可以到达更多目标的字节

1）****推断seed中受影响的bytes

独立相关性中的变量可以同时改变以接近不同的目标。因此，如果这些变量的值依赖于不同的字节，模糊器可以同时改变它们以生成多个目标的输入

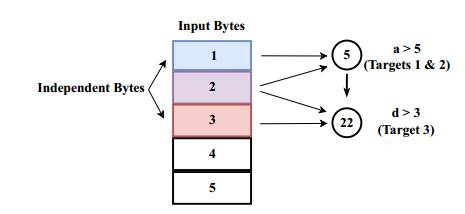
改变独立字节以提高输入生成效率的直觉。如果字节1和字节3同时发生突变，则fuzzers可以同时满足三个目标的两个条件，并且执行的次数更少。

2）****针对多个targets，变异这些bytes

根据它可以影响的靶点数量来确定字节的优先级。这是通过自适应方法实现的，其中我们首先推断每个靶点的字节，然后改变其重点输入字节

以概率p选择字节

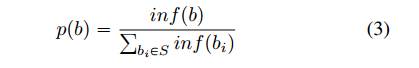
多元动态能量感知的种子分级技术

传统的模糊测试软件在对种子进行评分的过程中，基本只采取单一的种子评价标准。譬如AFL基于代码覆盖率进行种子评价，AFLGo基于基本块距离的种子评价。

现有种子分级方案考虑因素单一性带来了漏洞发现能力的局限，使得传统模糊测试工具无法满足特定场景下实现靶向挖掘的需求。

面对现有的技术难点，首先在传统的种子评价方法之上（比如：基本块距离、代码覆盖率、崩溃率等），基于效果驱动提出更多种子评价方法，包括种子的执行时间、位图大小（即该种子的覆盖率）、障碍（即该种子在队列中的落后周期数）、深度（即该种子是由多少次变异产生的，深度越高，表示该种子越复杂）、距离（即该种子距离目标函数的距离，距离越小，表示该种子越接近目标函数）、相似度（度衡量种子和目标之间执行轨迹相似程的指标，相似度越高，说明种子越有可能触发目标函数或者导致目标状态变化），形成全新的多元种子评价标准集合，并将之命名为多元融合模块。

多元融合模块指标计算部分的修改代码在afl-fuzz.c文件的5111-5267行:

//输入参数struct queue_entry* q: 指向待计算分数的测试用例结构体的指针，
//该结构体包含与测试用例相关的各种属性，如执行时间、位图大小、障碍值、深度等。
static u32 calculate_score(struct queue_entry* q) {

//计算测试用例的平均执行时间和平均位图大小
//total_cal_us 和 total_cal_cycles: 分别记录所有测试用例的累计执行时间和执行次数，用于计算平均执行时间。
//total_bitmap_size 和 total_bitmap_entries: 记录所有测试用例的总位图大小和参与统计的测试用例数量，用于计算平均位图大小。
  u32 avg_exec_us = total_cal_us / total_cal_cycles;
  u32 avg_bitmap_size = total_bitmap_size / total_bitmap_entries;

//初始化性能得分为100
  u32 perf_score = 100;
  /* Adjust score based on execution speed of this path, compared to the
     global average. Multiplier ranges from 0.1x to 3x. Fast inputs are
  less expensive to fuzz, so we're giving them more air time. */
//根据 q->exec_us（当前测试用例的执行时间）与 avg_exec_us 的关系，按一定规则调整 perf_score得分
//这种设计逻辑是认为执行速度快的测试用例在相同时间内可以尝试更多变异，因此给予更高的分值以增加其变异机会。
  if (q->exec_us * 0.1 > avg_exec_us) perf_score = 10;
  else if (q->exec_us * 0.25 > avg_exec_us) perf_score = 25;
  else if (q->exec_us * 0.5 > avg_exec_us) perf_score = 50;
  else if (q->exec_us * 0.75 > avg_exec_us) perf_score = 75;
  else if (q->exec_us * 4 < avg_exec_us) perf_score = 300;
  else if (q->exec_us * 3 < avg_exec_us) perf_score = 200;
  else if (q->exec_us * 2 < avg_exec_us) perf_score = 150;
  /* Adjust score based on bitmap size. The working theory is that better
     coverage translates to better targets. Multiplier from 0.25x to 3x. */
//根据 q->bitmap_size（当前测试用例的位图大小）与 avg_bitmap_size 的关系，按一定规则调整 perf_score得分
//假设位图大小与覆盖质量正相关，具有更大位图的测试用例更可能发现新的路径和漏洞，因此给予更高的分值。
  if (q->bitmap_size * 0.3 > avg_bitmap_size) perf_score *= 3;
  else if (q->bitmap_size * 0.5 > avg_bitmap_size) perf_score *= 2;
  else if (q->bitmap_size * 0.75 > avg_bitmap_size) perf_score *= 1.5;
  else if (q->bitmap_size * 3 < avg_bitmap_size) perf_score *= 0.25;
  else if (q->bitmap_size * 2 < avg_bitmap_size) perf_score *= 0.5;
  else if (q->bitmap_size * 1.5 < avg_bitmap_size) perf_score *= 0.75;
  /* Adjust score based on handicap. Handicap is proportional to how late
     in the game we learned about this path. Latecomers are allowed to run
     for a bit longer until they catch up with the rest. */
 //q->handicap 表示当前测试用例相对于其他已知测试用例的“落后”程度，即其在何时被发现并加入队列。晚到的测试用例可能因为未充分探索而具有潜在的高价值。
 if (q->handicap >= 4) {
    perf_score *= 4;
    q->handicap -= 4;
  } else if (q->handicap) {
    perf_score *= 2;
    q->handicap--;
  }
  // /* Final adjustment based on input depth, under the assumption that fuzzing
  // deeper test cases is more likely to reveal stuff that can't be
  //   discovered with traditional fuzzers.
  //   * /
//q->depth 表示当前测试用例的深度（即该种子是由多少次变异产生的）
//深度较大的测试用例可能触发更深层次的代码逻辑或异常情况，赋予更高的分数
  switch (q->depth) {
  case 0 ... 3:   break;
  case 4 ... 7:   perf_score *= 2; break;
  case 8 ... 13:  perf_score *= 3; break;
  case 14 ... 25: perf_score *= 4; break;
  default:        perf_score *= 5;
  }
//调用 get_cur_time() 函数获取当前的系统时间
//t 现在代表模糊测试自启动以来已经运行的秒数。
  u64 cur_ms = get_cur_time();
  u64 t = (cur_ms - start_time) / 1000;
//将执行的总时间除以预期时间，一个介于 0.0 和 1.0 之间的浮点数，表示当前进度占目标时间的比例。
  double progress_to_tx = ((double)t) / ((double)t_x * 60.0);
//根据上一步得到的执行的进度，确定冷却计划，计算当前的温度，即 T
//温度是一个介于 0 和 1 之间的数，表示执行的热度，温度越高，表示执行越热，越容易接受较差的种子。温度的计算方式根据冷却计划的不同而不同
  double T;
  //TODO Substitute functions of exp and log with faster bitwise operations on integers
  switch (cooling_schedule) {
  case SAN_EXP:
    T = 1.0 / pow(20.0, progress_to_tx);
    break;
  case SAN_LOG:
    // alpha = 2 and exp(19/2) - 1 = 13358.7268297
    T = 1.0 / (1.0 + 2.0 * log(1.0 + progress_to_tx * 13358.7268297));
    break;
  case SAN_LIN:
    T = 1.0 / (1.0 + 19.0 * progress_to_tx);
    break;
  case SAN_QUAD:
    T = 1.0 / (1.0 + 19.0 * pow(progress_to_tx, 2));
    break;
  default:
    PFATAL("Unkown Power Schedule for Directed Fuzzing");
  }
//定义两个双精度浮点数变量 power_factor 和 power_factor_sim，初始化为 1.0，
它们分别用于表示距离和相似度对性能得分的影响因子。
//定义一个双精度浮点数变量 normalized_d，初始化为 0，用于存储归一化后的距离值。
  double power_factor = 1.0, power_factor_sim = 1.0;
  double normalized_d = 0;
//	归一化的方式是将距离或相似度减去最小值，再除以最大值和最小值的差。如果最大值和最小值相等，那么归一化的值为 0，表示该条目的距离或相似度与其他条目没有差异。
  if (q->distance > 0) {
    // when "max_distance == min_distance", we set the normalized_d to 0 so that we can sufficiently explore those testcases whose distance >= 0.
    if (max_distance != min_distance)
      normalized_d = (q->distance - min_distance) / (max_distance - min_distance);
//如果 normalized_d 大于等于 0，则进一步计算一个基于 T（温度）和归一化距离的中间变量 p，并使用该 p 值以及一个预定义的最大因子 MAX_FACTOR 计算 power_factor。这里采用了对数和指数运算来构建一个非线性的映射关系，使得 power_factor 随 distance 和 T 的变化而变化。
//当距离越小，即越接近目标函数时，分数越高；当温度越高，即执行越热时，概率越低，以避免过早收敛到局部最优解。
    if (normalized_d >= 0) {
      double p = (1.0 - normalized_d) * (1.0 - T) + 0.5 * T;
      power_factor = pow(2.0, 2.0 * (double)log2(MAX_FACTOR) * (p - 0.5));
    }// else WARNF ("Normalized distance negative: %f", normalized_d);
  }
//定义另一个双精度浮点数变量 normalized_d_sim，初始化为 0，用于存储归一化后的相似度值。
  double normalized_d_sim = 0;
  if (q->sim > 0) {
    // when "max_sim == min_sim", we set the normalized_d to 0 so that we can sufficiently explore those testcases whose distance >= 0.
//如果最大相似度 max_sim 与最小相似度 min_sim 不相等，则计算测试用例相似度与相似度范围（max_sim - min_sim）的比值，得到归一化相似度 normalized_d_sim；否则，直接令 normalized_d_sim 等于 1。
    if (max_sim != min_sim)
      normalized_d_sim = (q->sim - min_sim) / (max_sim - min_sim);
    else normalized_d_sim = 1;
    if (normalized_d_sim >= 0) {
//如果 normalized_d_sim 大于等于 0，则将其转换为双精度浮点数 p_sim，并使用该 p_sim 值以及一个预定义的最大因子 MAX_FACTOR_SIM 计算 power_factor_sim。同样采用对数和指数运算构建非线性映射，使 power_factor_sim 随 sim 变化。
//当相似度越大，赋予的分数越高
      double p_sim = (double)normalized_d_sim;
      power_factor_sim = pow(2.0, 2.0 * (double)log2(MAX_FACTOR_SIM) * (p_sim - 0.5));
    }// else WARNF ("Normalized distance negative: %f", normalized_d);
  }
//将原来的 perf_score 与计算得到的 power_factor 和 power_factor_sim 相乘，得到新的性能得分，该得分综合考虑了测试用例的距离和相似度信息。
  perf_score *= power_factor * power_factor_sim;
  /* Make sure that we don't go over limit. */
//对更新后的 perf_score 进行检查，如果超过了一个预定义的最大值 HAVOC_MAX_MULT * 100，则将其设置为这个最大值，防止得分过高导致后续处理失衡。
  if (perf_score > HAVOC_MAX_MULT * 100) perf_score = HAVOC_MAX_MULT * 100;
  /* AFLGO-DEBUGGING */
  // fprintf(stderr, "[Time %llu] q->distance: %4lf, max_distance: %4lf min_distance: %4lf, T: %4.3lf, power_factor: %4.3lf, adjusted perf_score: %4d\n", t, q->distance, max_distance, min_distance, T, power_factor, perf_score);
//记录并保存模糊测试过程中测试用例的关键属性（如相似度、距离、执行时间、影响因子、性能得分、时间戳和温度）到一个 CSV 文件中。
  FILE* file = fopen("./queue.csv", "a");
  if (file) {
    fprintf(file, "%f,%lf,%llu,%lf,%lf,%u,%llu,%lf\n",
      q->sim,
      q->distance,
      q->exec_us,
      power_factor_sim,
      power_factor,
      perf_score,
      t,
      T); 
    fclose(file);
  }
  return perf_score;